परमाणु संरचना क्या है? जानिए A-Z आसान भाषा में

हेलो दोस्तों आज हम लोग चैप्टर परमाणु संरचना के बारे में पढ़ेगे है। दोस्तों इसमें हम परमाणु मॉडल के बारे में जानेगे। परमाणु के बारे में मैंने पहले से आर्टिकल लिख रखा है तो अगर आप परमाणु के बारे में जानना चाहते है तो लिंक पर क्लिक करके उस पोस्ट पर जाकर पढ़ सकते है।

परमाणु संरचना क्या है? What is Atomic Structure in Hindi?

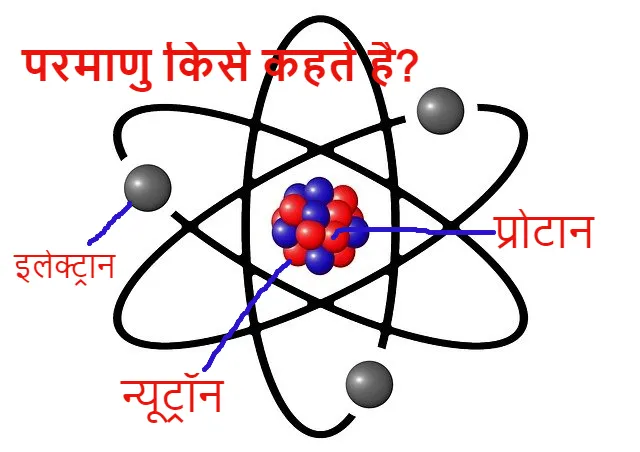
परमाणु की बनावट को ही परमाणु संरचना कहा जाता है इसी बनावट का अध्ययन करना ही परमाणु संरचना के अंतर्गत आता है

रदरफोर्ड का प्रयोग (Ruther ford’s Experiment) –

अल्फ़ा किरणे = अल्फा कण = ₂He⁴ = हीलियम नाभिक

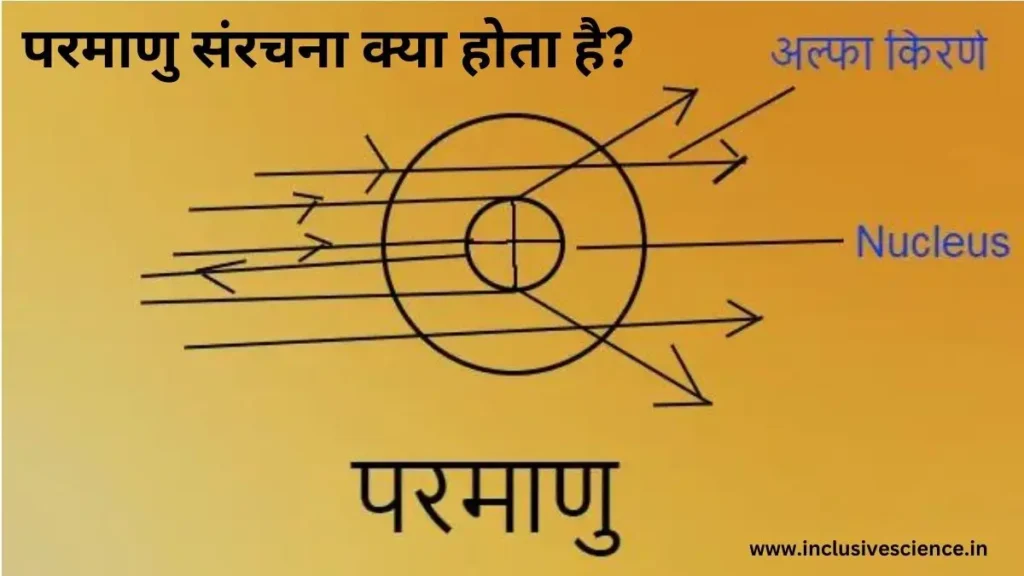
रदरफोर्ड नामक वैज्ञानिक ने धातु की पतली पन्नी (सोना, चाँदी) पर अल्फ़ा कणों की बम्बारी किया जिससे उन्होंने ने निम्नलिखित निष्कर्ष निकाले।

• अधिकांश अल्फा कण सीधे निकल जाती है। जिससे यह निष्कर्ष निकाला कि परमाणु का अधिकांश भाग खोखला है।
• जब अल्फा कणों की बम्बारी परमाणु केंद्र के समीप की जाती है, तो अल्फा कण अपने मार्ग से विचलित हो जाती है। जिससे उन्होंने स्पष्ट किया कि परमाणु के केंद्र में कोई धनावेशित भाग है।
• जब अल्फा कण की बम्बारी ठीक मध्य बिंदु पर की जाती है, तो एक या दो कण अपने मार्ग में वापस लौट आते है।
• परमाणु का समस्त भार तथा सम्पूर्ण धनावेश परमाणु के केंद्र में केन्द्रित या निहित होता है। जिसे परमाणु का नाभिक कहा जाता है।
• नाभिक पर कुल केन्द्रित धनावेश, इलेक्ट्रानो के कुल ऋणावेशों के बराबर होता है जिससे परमाणु में विद्दुत आवेशो का संतुलन बना रहता है और वह उदासीन रहता है
• इन्होने बताया की परमाणु में उपस्थित ऋणावेशित इलेक्ट्रान इसके धनावेशित नाभिक के चारो ओर घूमते रहते है
• नाभिक की त्रिज्या 10^-12 सेमी और परमाणु की त्रिज्या 10^-8 सेमी होती है इससे यह स्पष्ट होता है कि परमाणु की त्रिज्या नाभिक की त्रिज्या से लगभग 10,000 गुना अधिक होती है
• रदरफोर्ड के इस मॉडल को परमाणु का नाभिकीय मॉडल (nuclear model) कहा गया इस मॉडल को सौर या ग्रहीय मॉडल भी कहते है क्योकि इस मॉडल में यह कल्पना की गयी है कि जिस प्रकार सूर्य के चारो ओर ग्रह परिक्रमा करते है उसी प्रकार नाभिक के चारो ओर इलेक्ट्रान घूमते रहते है
• रदरफोर्ड वैज्ञानिक ने इस प्रकार परमाणु नाभिक की खोज की।

प्राचीन परमाणु मॉडल (Classical Atomic Model) –

प्राचीन परमाणु मॉडल इलेक्ट्रान की कण गुण पर आधारित है इसमें निम्नलिखित मॉडल प्रस्तुत है।

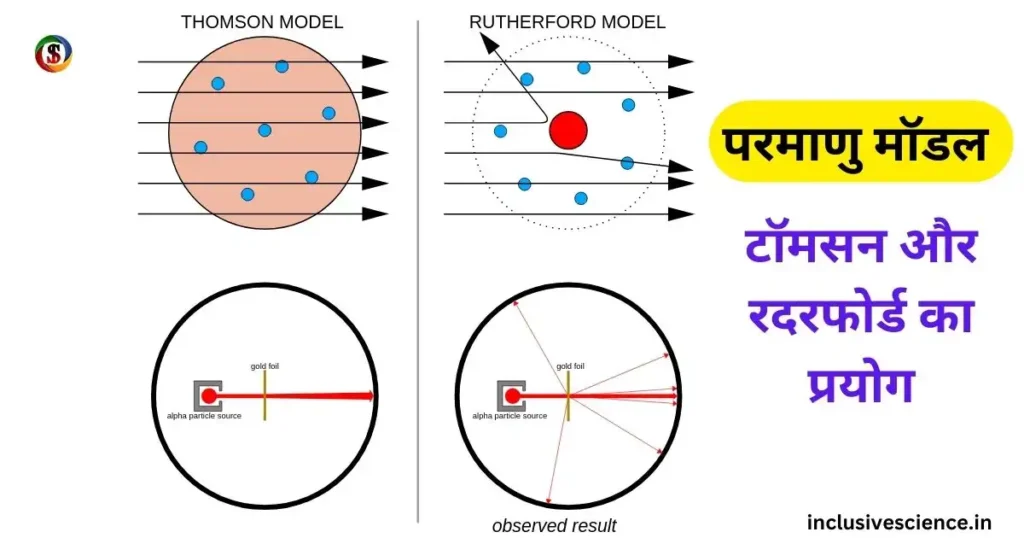
टॉमसन परमाणु मॉडल (Thomson Atomic Model) –

टॉमसन मॉडल प्रथम परमाणु मॉडल है।

टॉमसन के अनुसार –

परमाणु का आकार तरबूज के समान होता है। जिसमे खाने वाला भाग नाभिक होता है तथा इलेक्ट्रान बीज के रूप में धंसे रहते है।

समान आवेशो के मध्य लगने वाला प्रतिकर्षण बल, विपरीत आवेशो के मध्य लगने वाला आकर्षण बल द्वारा परमाणु संतुलित अवस्था में बना रहता है।

इन्होने परमाणु के विषय में कोई विशेष जानकारी नहीं दिया था अतः आगे चलकर यह मॉडल असफल हो जाता है।

रदरफोर्ड नाभिकीय मॉडल –

रदरफोर्ड मॉडल को प्रथम नाभिकीय मॉडल कहा जाता है।

Fa = Force of Attraction = आकर्षण बल

Fc = Centrifugal force = अपकेन्द्र बल

परमाणु का समस्त भार तथा सम्पूर्ण धनावेश परमाणु के केंद्र में केन्द्रित होता है। जिसे परमाणु नाभिक कहा जाता है। इसी नाभिक के चारो तरफ इलेक्ट्रान वृत्ताकार कक्षा में चक्कर लगाते है। इलेक्ट्रान पर नाभिक का लगने वाला आकर्षण बल इलेक्ट्रान बाहर की तरफ लगने वाले अपकेन्द्र बल से संतुलित बना रहता है।

नील बोर नामक बैज्ञानिक ने क्लार्क मैक्सवेल के अनुसार बताया कि कोई भी त्वरित आवेशित कण लगातार वैद्दुत चुम्बकीय विकिरण का उत्सर्जन करता है। जिससे इलेक्ट्रान की ऊर्जा कम होनी चाहिए। फलतः इलेक्ट्रान अपनी त्रिज्या को कम करता है और कम करते-करते अंत में परमाणु नाभिक में जा गिरता है। परन्तु ऐसा नही होता है। अतः रदरफोर्ड का परमाणु मॉडल असफल हो जाता है।

बोहर का परमाणु मॉडल (Bohr’s Model) –

बोहर का मॉडल रदरफोर्ड के परमाणु मॉडल के नाभिक को स्वीकार करता है तथा रदरफोर्ड की कक्षाओ में संसोधन करता है। इस मॉडल के अनुसार परमाणु नाभिक के चारो ओर अनन्त ऊर्जा स्तर होते है। जिससे इलेक्ट्रान ऊर्जा को ग्रहण करके अथवा त्याग करके परमाणु नाभिक के तरफ वृत्ताकार कक्षा में परिक्रमा करता है।

इलेक्ट्रान उस कक्षा में चक्कर में लगाते है। जिसका कोणीय संवेग nh/2π का पूर्ण गुणज होता है।

       mvr = nh/2π

जहाँ    m = इलेक्ट्रान का द्रव्यमान

       v = इलेक्ट्रान का वेग

       r = इलेक्ट्रान की नाभिक से दूरी अर्थात त्रिज्या

       n = 1, 2, 3…पूर्णांक संख्या

       h = प्लांक नियतांक

इलेक्ट्रान जिस ऊर्जा स्तर में चक्कर लगाता है। उसे कोश अथवा कक्षा अथवा मुख्य ऊर्जा स्तर अथवा स्थाई कक्षक मुख्य क्वांटम संख्या कहा जाता है।

इलेक्ट्रान ऊर्जा का अवशोषण करके अथवा उत्सर्जन करके अपनी कक्षाओ को बदल सकता है।

       delta E = E₂ – E₁

       n/ λ = E₂ – E₁

delta E = ऊर्जा में परिवर्तन

E₂ = उच्च ऊर्जा स्तर की ऊर्जा

E₁ = निम्नतम ऊर्जा स्तर की ऊर्जा

बोहर मॉडल में मुख्य क्वांटम संख्या तथा स्पेक्ट्रम की उत्पत्ति हुई थी।

बोहर का परमाणु मॉडल एकल इलेक्ट्रान वाले परमाणुओं अथवा आयनों के लिए लागू होता है।

उदाहरण – H, He⁺, Li⁺², Be⁺³

बोहर का परमाणु मॉडल परमाणु की अतिसूक्ष्म संरचना जीमान प्रभाव तथा स्टार्क प्रभाव आदि की व्याख्या नही कर पाता है।

NEET के लिए कम्पलीट नोट्स बुक –

NEET Teachers के द्वारा एकदम सरल भाषा में लिखी गई नोट्स बुक 3 in 1, यानि कि एक ही किताब में जीव विज्ञान, रसायन विज्ञान और भौतिक विज्ञान की कम्पलीट कोर्स। यदि आपको इसकी जरूरत है तो नीचे दिए गये बुक इमेज पर क्लिक कीजिये और इसके बारे में और भी जानिए।

त्रिज्या, वेग, तथा ऊर्जा (Radius, Velocity and Energy) –

बोहर के परमाणु मॉडल के अनुसार किसी भी इलेक्ट्रान की n वी कक्षा में त्रिज्या वेग तथा ऊर्जा ज्ञात की जा सकती है।

       rn = n वी कक्षा में त्रिज्या

       rn = 0.529*n²/ Z (ऐन्गस्ट्राम में)

n = कक्षों की संख्या

z = तत्व का परमाणु क्रमांक

rn का मान ऐन्गस्ट्राम में होता है।

vn = n वीं कक्षा में इलेक्ट्रान का वेग

       Vn = 2.188*10⁸*z / n ओम / सेकंड

En = n वीं कक्षा में इलेक्ट्रान (e)^– की ऊर्जा

En = -Rhc*Z² / n²

R = Rydberg Constant = रिडबर्ग नियतांक

R = 1.097*10⁷ m^-1 (प्रतिमीटर)

h = प्लांक नियतांक

h = 6.67*10^-34 जूल – सेकंड

c = प्रकाश का वेग = 3*10⁸ m/sec

Rhc = 2.18*10^-18 J/Atom

Rhc = 2.18*10^-11 erg/Atom

Rhc = 13.6 ev/Atom

सोमर फील्ड मॉडल (Somerfeld model) –

सोमर फील्ड मॉडल बोहर की कक्षाओ में संसोधन किया था। इस मॉडल के अनुसार जब इलेक्ट्रान नाभिक के समीप होता है तो इलेक्ट्रान की कक्षा दीर्घ वृत्ताकार होती है और जब इलेक्ट्रान नाभिक से दूर होता है तो उसकी कक्षा वृत्ताकार होती है।

वृत्ताकार कक्षा में इलेक्ट्रान का कोणीय संवेग nh/2π होता है। जबकि दीर्घ वृत्ताकार कक्षा में इलेक्ट्रान का कोणीय संवेग kh/2π होता है।

n = Principal Quantum number (shell) {मुख्य क्वांटम संख्या (कोश)}

K = Azimuthal Quantum number (subshell) {द्विगंशी क्वांटम संख्या (उपकोश)}

आगे चलकर द्विगंशी क्वांटम संख्या K को l में बदल दिया गया।

सोमर फील्ड मॉडल में द्विगंशी क्वांटम संख्या की उत्पत्ति हुई जो कि इलेक्ट्रानो के उपकोशो को व्यक्त करता है।

सोमर फील्ड मॉडल परमाणुओं की अतिसूक्ष्म संरचना, जीमान प्रभाव, स्टार्क प्रभाव आदि की व्याख्या करता है। चुम्बकीय क्षेत्र में स्पेक्ट्रमी रेखाओ का विघटन जीमान प्रभाव कहलाता है। जबकि बैद्दुत क्षेत्र में स्पेक्ट्रमी रेखाओ का विघटन स्टार्क प्रभाव (Stark Effect) कहलाता है।

प्राचीन परमाणु मॉडल इलेक्ट्रान की कण प्रकृति पर आधारित है। 

आधुनिक परमाणु मॉडल (Modern Atomic Model) –

आधुनिक परमाणु मॉडल इलेक्ट्रान के कण प्रकृति तथा तरंग प्रकृति पर आधारित होता है। डी ब्रोग्ली नामक बैज्ञानिक ने बताया की इलेक्ट्रान में कण गुण तथा तरंग गुण दोनों विद्यमान होते है। अतः स्पष्ट होता है कि इलेक्ट्रान की प्रकृति द्वैती प्रकृति होती है।

अल्बर्ट आइन्स्टीन (Albert Einstein) के द्रव्यमान ऊर्जा समीकरण के अनुसार –

       E = mc² ———–(1)

प्लांक नामक बैज्ञानिक के अनुसार –

       E = hv

       E = hc/λ  (चुकी v = c/λ) ————-(2)

V = न्यू = Freqency of Light (प्रकाश की आवृत्ति)

C = प्रकाश की चाल

समीo (1) और समीo (2) से तुलना करने पर

mc² = hc/λ

mc²      = hc/λ

λ = h/mc

जब किसी सूक्ष्म कण को प्रकाश का वेग प्रदान किया जाता है तो वह कण तरंगे उत्पन्न करता है।

       V = कण की चाल

       C = प्रकाश की चाल

       C = V

λ = h/mv = h/p   यही डी ब्राग्ली का समीकरण है।

λ = प्रकाश की तरंग दैर्ध्य है।

टॉमसन मॉडल, रदरफोर्ड मॉडल, बोहर मॉडल, सोमरफील्ड मॉडल आदि। मॉडल इलेक्ट्रान की कण पर आधारित है। बोहर मॉडल में इलेक्ट्रान का कोणीय संवेग nh/2π होता है।

इसी प्रकार इलेक्ट्रान के तरंग मॉडल में इलेक्ट्रान का कोणीय संवेग nh/ 2π होता है।

एक तरंग की लम्बाई तरंग दैर्ध्य कहलाती है। यदि इलेक्ट्रान एक चक्रण में n तरंगे उत्पन्न करता है। तो –

 n तरंग की लम्बाई = nλ

n तरंगो की लम्बाई वृत्त की परिधि के बराबर होती है।

 n तरंग की लम्बाई = वृत्त की परिधि

  nλ = 2πr

जहाँ r वृत्त की त्रिज्या है।

       λ = h/ mv

       nh/ mv = 2πr

       mvr = nh/ 2π

mvr = इलेक्ट्रान का कोणीय संवेग ।

हाइजेनबर्ग का अनिश्चिता सिद्धांत (Heigenberg Uncertainity Principal) –

किसी भी गतिशील इलेक्ट्रान के लिए एक ही समय पर संवेग तथा स्थिति का निर्धारण नहीं किया जा सकता है। इसका अर्थ है या तो संवेग में अनिश्चिता पायी जाती है या तो स्थिति में अनिश्चिता पायी जाती है।

       डेल्टा p = delta x ≥ h/ 4π

हाइजेनबर्ग के समीकरण के अनुसार रेखीय संवेग में अनिश्चिता तथा स्थिति में अनिश्चिता का गुणनफल या तो h/ 4π के बराबर है और h/ 4π से अधिक है।

       p = mv

       delta p = m delta v

       m delta v.delta x = h/ 4πm

इस समीकरण के अनुसार गतिशील इलेक्ट्रान के वेग में अनिश्चिता तथा स्थिति में अनिश्चिता का गुणनफल या तो h/ 4πm के बराबर है अथवा h/ 4πm से अधिक है।

       delta p = गतिशील इलेक्ट्रान के संवेग में अनिश्चिता

       delta x = गतिशील इलेक्ट्रान के स्थिति में अनिश्चिता

       delta v = गतिशील इलेक्ट्रान के वेग में अनिश्चिता

Conclusion –

दोस्तों चलो देख लेते है। कि इस पोस्ट में हम लोगो ने किन – किन चीजो के बारे में जाना।

रदरफोर्ड का प्रयोग, प्राचीन परमाणु मॉडल, टॉमसन परमाणु मॉडल, रदरफोर्ड नाभिकीय मॉडल, बोहर का परमाणु मॉडल, त्रिज्या, वेग, ऊर्जा, सोमर फील्ड का परमाणु मॉडल, आधुनिक परमाणु मॉडल, हाइजेनबर्ग का अनिश्चिता सिद्धांत के बारे में अच्छी तरह से जाना।

तो दोस्तों आपको यदि परमाणु संरचना के बारे में दी गई जानकारी पसंद आयी हो तो प्लीज इसे अपने दोस्तों के साथ अधिक से अधिक शेयर कीजिये।

धन्यवाद